Kedves Vendégem!

Honlapom választott témája első látásra unalmasnak tűnik. Azt szokták mondani, hogy a prímszámok világa, a prímekkel kapcsolatos törvényszerűségek ismerete nélkül is jól megvagyunk. Azok talán csak újabban, a társadalmi, gazdasági élet titkosítási kívánalmainak megoldására nyújtanak lehetőséget. Sokáig magam is így gondoltam, sokkal jobban érdekeltek a mindnyájunkat körülvevő és bennünk is élő természet csodái. Hiszen, ha nyitott szemmel és nyitott szívvel járva bármerre tekintünk, a galaxisok makro világában, az elemi részecskék mikrovilágában, az élettelen és élő természet változatosságában megláthatjuk a rendezetlen állapot rendjét, harmóniáját. Észrevehetünk csodálatos szimmetriákat, fraktál jelenségeket, és töprenghetünk a végtelenség titkán.

A tudósoktól megtudhatjuk, hogy ezeknek a rendszereknek a kapcsolata és egyáltalán a működőképessége, léte, csak az azokat leíró összefüggések fő paramétereinek szigorú, pontos állandósága mellett lehetséges. Ha ezek a paraméterek csak a legkisebb mértékben is eltérnének a ténylegestől, világunk összeomlana, és arra már nincsen reális elképzelés, hogy mi lenne helyette.

A természet csodálata mindig megmentett az unalomtól. Amikor életem egy kevésbé aktív szakaszában négyzethálós papírlap felett elkezdtem az egész számokat a számegyenes helyett síkfelületen ábrázolni,  éreztem, hogy a prím- és összetett számok egybefonódó, végtelen sora kapcsolatban van a természet jelenségeivel   (Függelék IP 1. ábra) .  

Szembeötlő volt a 2, a 3 és a 2*3=6 szám szerepe a szimmetriák világában. Később megtudhattam, hogy a prím- és összetett számok véletlenszerűnek tűnő sorrendje zenei harmóniákat tükröz. 

A prímszámok között sokféle egyszerű összefüggés is található. Ezek egy része prímszám-párokra vonatkozik, és régóta bizonyításra vár. Általános értelmezés szerint a sorrendben egymást követő két prímet tekintjük párnak, tehát valamely prímhézagot közvetlenül megelőző és követő két prímet. Bizonyítható, hogy a számok sorrendjében a nagy számok felé haladva, bár viszonylag egyenletesnek látszik a prímek számának növekedése, a prímhézagok mérete minden korlátot meghaladhat. Ugyanakkor Eukleidész óta (kb. 2300 éve) bizonyításra vár az egyszerű sejtés, hogy a legkisebb prímhézagok száma végtelen sok (ikerprím-sejtés). Bonyolult matematikai módszerekkel sikerült már az igen nagy prímhézagok végtelen számának bizonyítása és a hézagok méretének szűkítése felől közelíteni a probléma megoldását. Honlapom elsődlegesen a 2 különbségű ikerprímek végtelen számának bizonyítására elemi matematikai módszereket mutat be, utalva arra, hogy várhatóan analóg módon lehet bizonyítani a 4 különbségű unokatestvér prímek végtelen számát is.

Más, tágabb értelmezés szerint bármely két prímet párnak tekinthetünk. Ebben semmi különös nincsen, mégis, több évszázados (1742. óta) be nem bizonyított sejtés, hogy minden természetes összetett szám pozitív prímszám-pár/prímszám-párok számtani középértéke. Goldbach sejtése: minden 2-nél nagyobb páros szám felbontható legalább 1 pozitív prímszám-pár összegére (itt két azonos prím is alkothat párt). Az összegezve páros számot eredményező prímszám-párok száma erősen szóródó értékeket mutat (Goldbach-üstökös, l. alább), amelyeknek természetesen van felső korlátja, de véletlenszerű előfordulást feltételezve, alsó korlát is állítható. Az alsó korlát függvénye/függvényei a Goldbach-sejtés szigorítását jelenti/jelentik. A Goldbach-üstökös 3 fő pászmája az egész számok sorának 6 végtelen számtani sorozatra bontásával adódó 3 páros szám sorozatnak felel meg:
                                         prímszám-párok száma 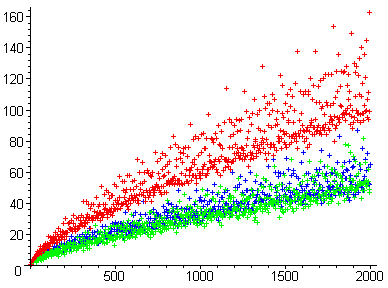                                                                                                                             páros számok
                                                             (KÖMAL Fórum: A Goldbach-sejtésről, [993] hozzászólás) 

Meglátásom szerint, ha célunk a prímszámokra vonatkozó összefüggések feltárása, akkor az összetett számok közötti kapcsolatok ismeretéből kiindulva érhetünk el eredményt. Ha az élő és élettelen természet jelenségei és létformái valóban összefüggenek a prím- és összetett számok törvényszerűségeivel, akkor a Teremtő tökéletesen ismeri és alkalmazza a matematikát.

                                                                          Soli Deo Gloria!